Image Generation with a Sphere Encoder

Kaiyu Yue* 1 2, Menglin Jia* 1, Ji Hou1, Tom Goldstein2
Meta1, University of Maryland2
*Equal contribution
arXiv Code (coming soon)

Uniformity on the Sphere. Our Sphere Encoder maps the natural image distribution uniformly onto a global sphere. The decoder then generates an image by decoding a point on the sphere. Shown here for three random classes of CIFAR-10, latents from CIFAR-10 training samples are projected into 3D via a random Gaussian matrix and normalized to unit length. The distribution reveals a highly uniform coverage of the sphere within each class, a trend consistent across various datasets, such as ImageNet, Animal-Faces, and Oxford-Flowers. This uniformity is valid for both conditional and unconditional models.


We introduce the Sphere Encoder, an efficient generative framework capable of producing images in a single forward pass and competing with many-step diffusion models using fewer than five steps. Our approach works by learning an encoder that maps natural images uniformly onto a spherical latent space, and a decoder that maps random latent vectors back to the image space. Trained solely through image reconstruction losses, the model generates an image by simply decoding a random point on the sphere. Our architecture naturally supports conditional generation, and looping the encoder/decoder a few times can further enhance image quality. Across several datasets, the sphere encoder approach yields performance competitive with state of the art diffusions, but with a small fraction of the inference cost.

Sphere Encoder, trained entirely from scratch, can generate sharp and high-fidelity images in within 4 steps.



Latent Space Spherification

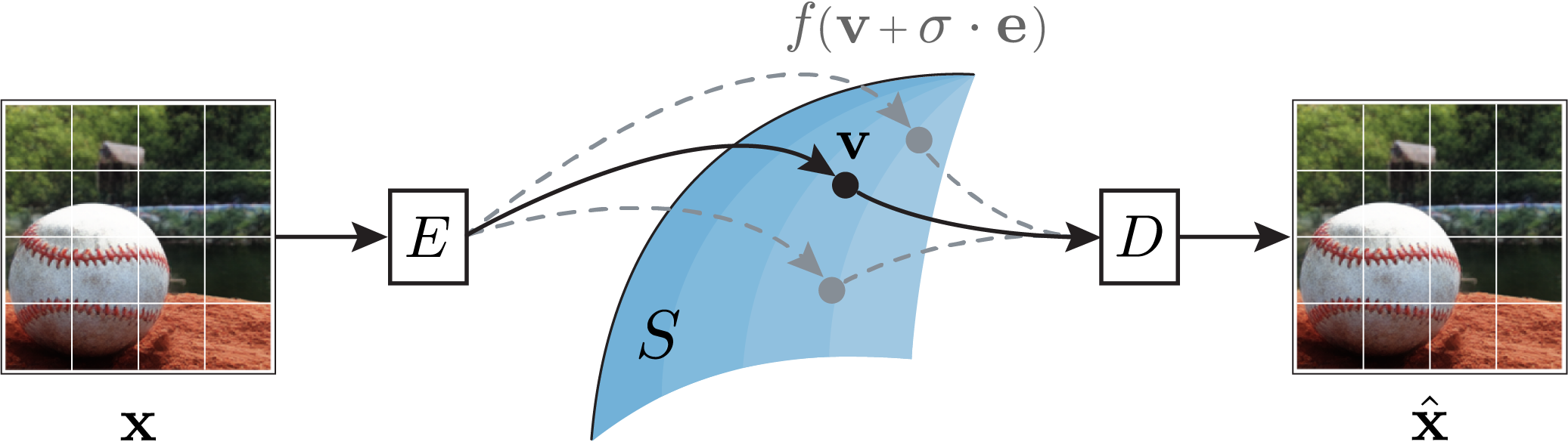
Spherifying latent with noise diagram

Spherifying the latent space with noise. Encoder E maps image x to a latent, which f projects to v on sphere S. During training, random Gaussian noise σ·e is added to v, where σ is jittered magnitude. Decoder D reconstructs the image from the re-projected noisy latent f(v + σ·e).



Overcoming the Posterior Hole Problem

Swipe to compare different models against the "Posterior Hole" problem.
Columns show: (1) Input images; (2) Autoencoder reconstructions; (3) Samples from standard Gaussian prior; and (4) Samples from estimated Gaussian posterior on the training set of Animal-Faces.

Variational Autoencoders (VAEs) face a fundamental trade-off: the divergence loss (matching a Gaussian prior) and the reconstruction loss are often at odds. Minimizing one typically degrades the other, leading to "posterior holes"—regions in the latent space that do not map to valid images.

Modern VAEs

Attempt to force latents into a Gaussian distribution. This creates a conflict where the learned posterior fails to match the prior, making direct sampling unreliable.

Sphere Encoder

Forces latents onto a uniform spherical manifold. By spreading embeddings away from each other on a bounded sphere, we achieve uniformity without sacrificing reconstruction accuracy.



Latent Interpolation

As we move through learned latent space, our model exhibits fast/sudden transitions between image classes rather than producing ``hybrid'' images that unrealistically merge properties of difference object types. For example, starting with the bottom-left image of a cheetah, we observe a sudden transition from cheetah to cat as we move vertically, and from cheetah to dog as we move horizontally. The model does not linger in a half-cheetah/half-dog state that is absent in the training data. These fast-transitions are necessary for a model to reliably convert random samples from the sphere into realistic images, as it makes the probability of observing a hybrid image small.

This important property of the sphere encoder differentiates it from other latent models. GANs, for example, tend to exhibit slow transitions, resulting in frequent production of hybrid or distorted objects, e.g., Figure 8 and 9 in BigGAN.



Image Editing

Sphere encoder enables versatile image editing capabilities across various scenarios, from OOD transformations to composite harmonization. A key benefit of this approach is that the entire editing process is training-free, allowing for high-quality manipulation without the need for additional fine-tuning or task-specific optimization.


Transforming Out-of-Distribution Images

conditional manipulation

Given an image far outside of the training distribution, we repeatedly encode and decode an input image, conditioning on different ImageNet classes.

We observe that a single step captures the primary object from the input while adapting its texture to match the target class. By increasing the iterations (e.g., 4-step generation), the model further refines the object's texture and key characteristics to align with the target class—all while maintaining the structural integrity of the original image.

Transforming Stitched Composites

cross over

We further demonstrate the model's editing capabilities by manually stitching together two distinct sources, Image A and Image B. By repeatedly encoding and decoding this stitched composite, the model naturally smooths the boundaries and harmonizes the content.

The process forces the manipulated image to converge to a valid point on the learned spherical manifold. Notably, unlike diffusion models (which require noise injection to hallucinate details), our encoder directly projects the stitched image into the latent space without adding noise, preserving the semantic integrity of both original images while creating a seamless transition.



Uncurated Generated Images



Acknowledgements

We would like to thank Tan Wang, Chenyang Zhang, Tian Xie, Wei Liu, Felix Juefei Xu, and Andrej Risteski for valuable discussion and feedback.

BibTeX

@article{kai2026sphere,
  title  = {Image Generation with a Sphere Encoder},
  author = {Yue, Kaiyu and Jia, Menglin and Hou, Ji and Goldstein, Tom},
  journal= {arXiv preprint arXiv:2602.15030},
  year   = {2026}
}